Pièces
Bondisseurs
Un Bondisseur est ainsi appelé parce qu’il ne se déplace que par bonds. Partant d’une case donnée, un Bondisseur peut atteindre, au choix, un certain nombre de cases. Pour le définir, on pourra donner pour chaque case de départ, la liste des cases d’arrivée possibles. Mais pour définir de façon simple ces ensembles de cases, et donc donner une définition concise de la pièce, il est plus intéressant de donner une formule.
Formule du Bondisseur simple
La définition d’un Bondisseur simple repose sur une formule mathématique simple : les coordonnées de la case d’arrivée de chaque mouvement de ce Bondisseur sont deux entiers (positifs, négatifs ou nuls) constants.
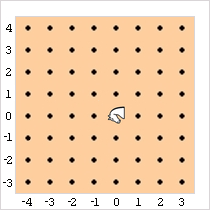
Diagramme A : Chaque case de départ du Bondisseur est, par convention, le point de coordonnées zéro et zéro. Ici, c’est la case e4.
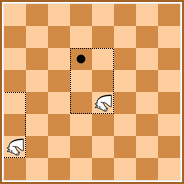
- Diagramme B
- Le Bondisseur simple-(-1,2) e4 peut jouer en d6.
De a2, il ne peut pas jouer.
Diagramme B : Si les coordonnées du Bondisseur simple sont -1 et 2, alors depuis « e4 » il peut jouer à « d6 », case de coordonnées -1 et 2. On dira que c’est le Bondisseur simple-(-1,2). S’il est placé sur une case de la première colonne, ici « a2 », il ne peut pas se déplacer. En effet, la case « a2 » devient la case (0,0), mais la case (-1,2) n’existe pas. De même, un Bondisseur simple-(-1,2) placé sur une des cases des septième et huitième traverses ne peut pas jouer.
L’ordre des nombres entre parenthèses n’est pas indifférent. Le premier correspond à l’abscisse du point d’arrivée (déplacement le long de la traverse), le second à son ordonnée (déplacement le long de la colonne).
En pratique, on ne renumérote pas les cases à chaque coup. Dans l’exemple précédent, la case « e4 » reste la case de coordonnées 5 et 4. On retire 1 à 5 et on ajoute 2 à 4 pour obtenir les coordonnées de la case d’arrivée (case « d6 » de coordonnées 4 et 6).
Les mouvements d’un même Bondisseur simple sont équipollents.
On utilise les Bondisseurs simples pour définir des Bondisseurs plus complexes, comme les Bondisseurs réguliers.
equipollents
Ouvrage créé et géré à l'aide de SPIP, logiciel libre distribué sous Licence publique générale GNU (GNU GPL). Origine des images des pièces du jeu d'échecs et des échiquiers (Wikimedia Commons). D’autres informations : Echekk.