La longueur des coups (distance entre la case de départ et la case d’arrivée de la pièce qui joue ce coup) n’est pas une notion utile au jeu d’échecs orthodoxes. Ce qui compte, c’est le rapport entre les cases ; on peut voir l’échiquier comme un graphe. Il importe peu que l’on connaisse les dimensions des cases.

Il est question de la longueur des coups dans les définitions de certains genres féeriques. Voir la liste de ces genres grâce au mot-clé « Longueur des coups ».

On considère que l’échiquier est carré, que toutes les cases sont carrées et de même surface. Par convention, le côté d’une case a pour longueur 1, les pièces sont situées au centre de la case. La distance entre une pièce située en « a1 » et une pièce en « b1 », par exemple, est donc aussi égale à 1. La longueur d’un coup est la longueur de la ligne droite reliant les centres des cases de départ et d’arrivée. Pour calculer ces longueurs, on utilisera le théorème de Pythagore.

Par exemple, un coup de Cavalier aura la longueur de l’hypoténuse d’un triangle rectangle dont les autres côtés ont des longueurs de 1 et de 2. La longueur de l’hypoténuse est la racine carrée de la somme 1² + 2², soit √5. Voir aussi : Maximum.

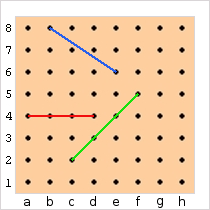
Diagramme A

Diagramme A :

• Le coup a4 → d4 a une longueur de 3 (ligne rouge)

• Le coup c2 → f5 a une longueur de √18 (ligne verte, 18 = 3² + 3²). c2-f5 est l’hypoténuse du triangle rectangle f2-c2-f5. Les deux autres côtés ont une longueur de 3

• Le coup b8 → e6 a une longueur de √13 (ligne bleue, 13 = 2² + 3²).

Genres

Les genres qui demandent que soit connue la longueur des coups sont nombreux, par exemple :

• Maximum : Les Noirs doivent jouer les coups les plus longs

• Minimum : Les Noirs doivent jouer les coups les plus courts

• Isométrique : Les Noirs doivent jouer des coups dont la longueur est égale à celle du coup blanc précédent

• Demi-isométrique : Les Noirs doivent jouer des coups dont la longueur est égale à la moitié de celle du coup blanc précédent.

Pièces

Le Bondisseur √25 (ou « Bondisseur 5 ») fait des bonds ayant une longueur égale exactement à 5. Ce sont tous les bonds de coordonnées 0 et 5, et tous ceux de coordonnées 3 et 4.

Le Bondisseur √50 fait des bonds ayant une longueur égale exactement à √50. Ce sont tous les bonds de coordonnées 5 et 5, et tous ceux de coordonnées 1 et 7.

Roques

La longueur du petit roque est égale à 4. On fait la somme des longueurs des déplacements du Roi et de la Tour qui le jouent. Celle du grand roque est donc de 5.